Kapitza Pendulum Simulation Research
Spring 2023
The goal of this research is to simulate how Kapitza Pendulum will behave when it is oscillating in an arc. An ordinary Kapitza Pendulum oscillates vertically. Without oscillation, the pendulum will be stable downwards. However, with oscillation, it’s able to hold an upright position. (Video Source: https://www.youtube.com/watch?v=GgYABmG_bto&ab_channel=DynamicsUci)
Vertical Oscillation
Before simulating Kapitza Pendulum with an arc-oscillating base, I started out with simulating vertical oscillation. The approach is the same for either vertical or arc oscillating base: define the system, derive Lagrange’s equation, calculate useful parameters, find the position at each time interval, and create an animation with all data points.
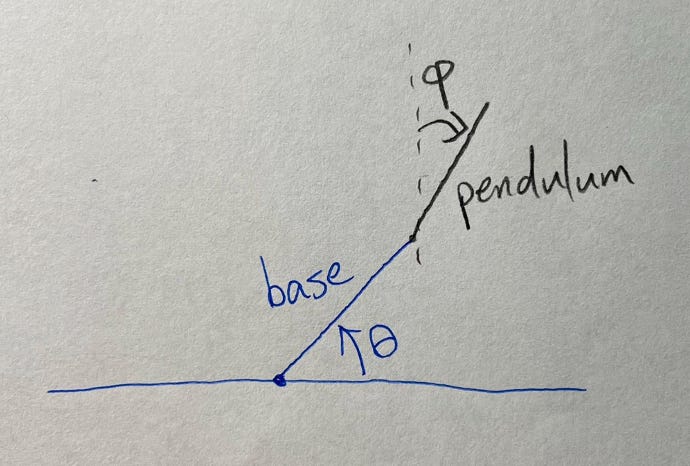
The image above represents the system setup of the vertically-oscillating Kapitza Pendulum. After having the system ready, I use the parameters to calculate Lagrange’s equation for this system.
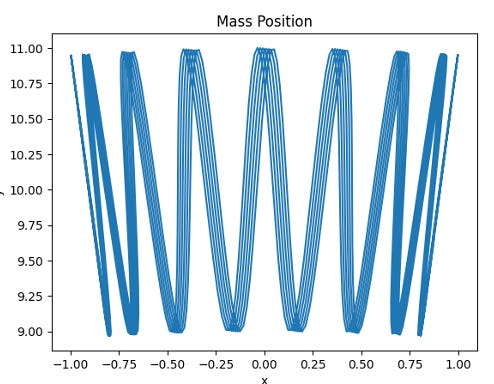
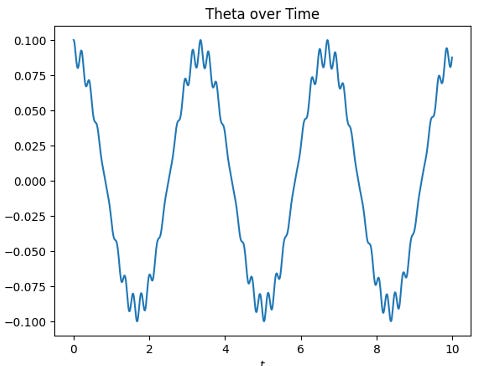
By using the derived Lagrange’s equation, I calculated the useful parameters for plotting the motion. Plotting out the position and theta over time is useful for debugging and pendulum behavior analysis.
As shown above, the motion of the pendulum is simulated with the animation. By adjusting the parameters (initial angle, oscillating angle, length, mass…) in the code, it’s able to simulate the pendulum under different conditions.
Arc Oscillation
By following the same steps as the vertically-oscillating Kapitza Pendulum, the setup and results of the Kapitza Pendulum with an arc-oscillating base are as follows:
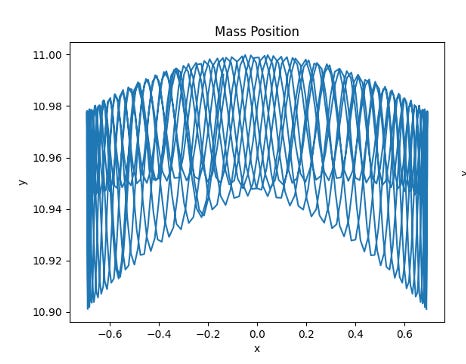
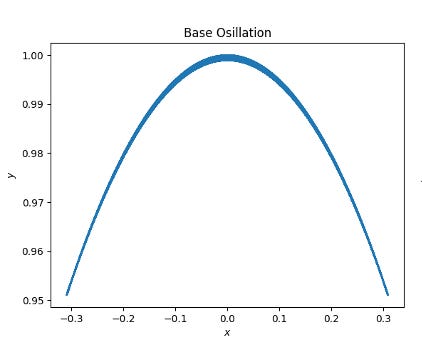
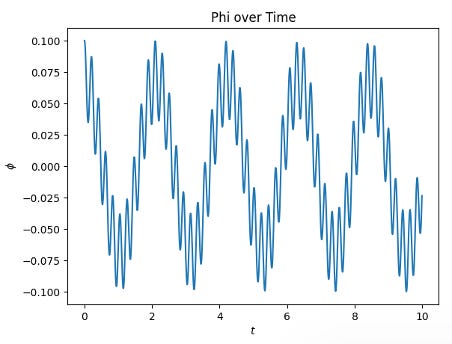
Even if the process is the same as the vertically-oscillating Kapitza Pendulum, there are still problems to overcome. For example, setting up an appropriate system is a hard task since it needs to be compatible for calculating its derivatives when deriving Lagrange’s equation. Calculating Lagrange’s equation is also difficult based on the complexity of the math. Since there are many possibilities of having an error in the result, I decided to use the arc-oscillating system to simulate vertical oscillation to see if it matches the result.
Arc-Oscillation Verification
Since I know the simulation of the vertically-oscillating Kapitza Pendulum is correct, I decided to have the arc-oscillating Kapitza Pendulum oscillate only in the vertical direction to see what the result is. To do this, I set the original rod position to be horizontal and set the oscillating angle to a small value. This way, the arc oscillation is so small that is approximately vertically oscillating. The simulation result is shown below.
Since the simulation of the vertically-oscillating Kapitza Pendulum using a 2D (arc) system correctly resembles the original vertical oscillation simulation, I decided that the simulation is correct and is ready to collect data for analysis.
Data Collection
The final step after verifying the accuracy of the arc-oscillation motion is to collect data by trying different combinations of the parameters. There are seven parameters: peak-to-peak angle of base oscillation, initial base angle, angular frequency of the arc-oscillating base, radius of the base, rod length, mass weight, and initial pendulum angle. To simplify the data collection process, we limit five of the variables and change only the peak-to-peak angle and the initial angle. The peak-to-peak angle changes from 0 < θpp ≤ π/2 and the initial angle varies by three values: 3π/4, π/2, and π/4. The collected data are shown below.
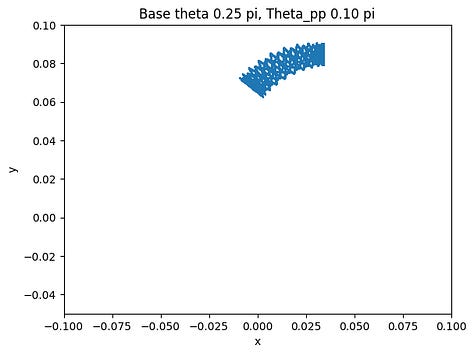
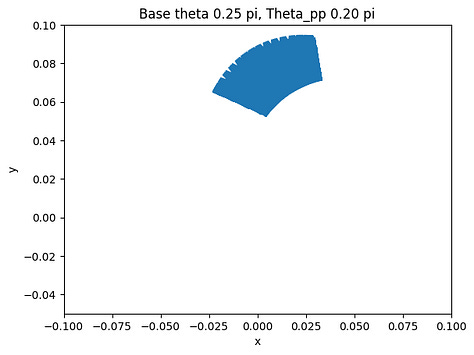
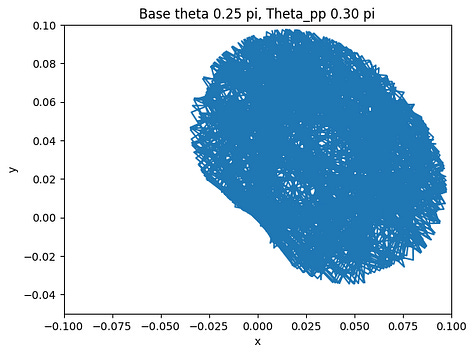
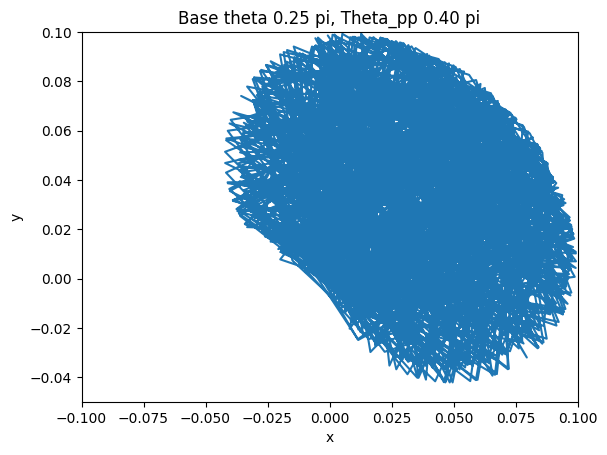
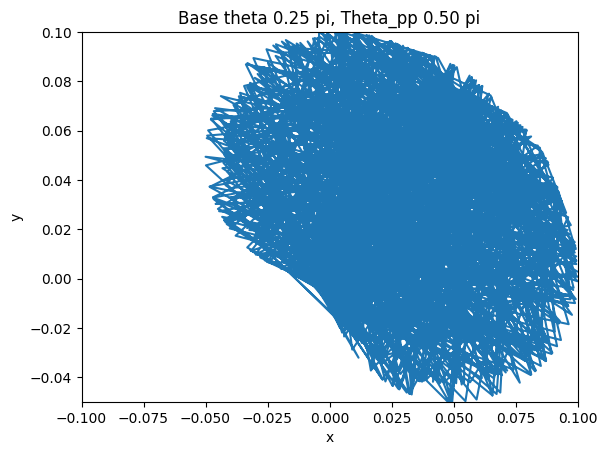
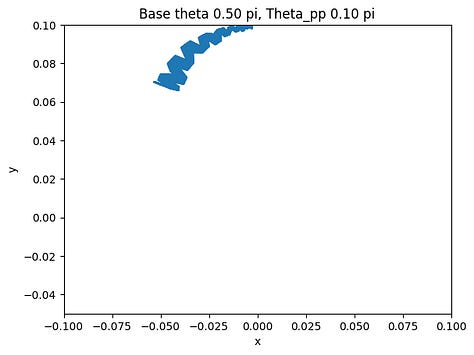
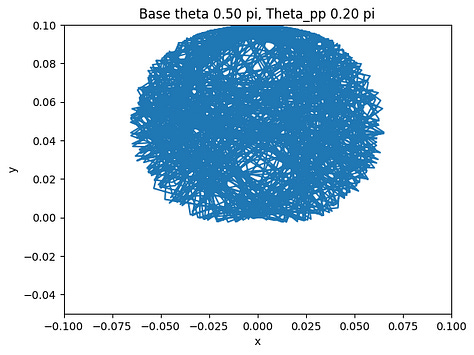
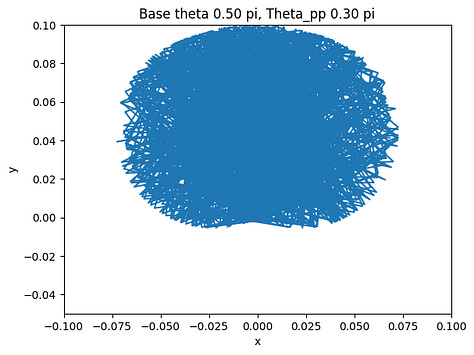
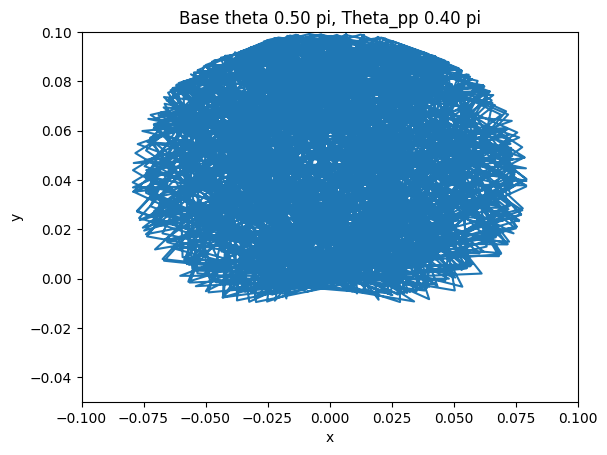
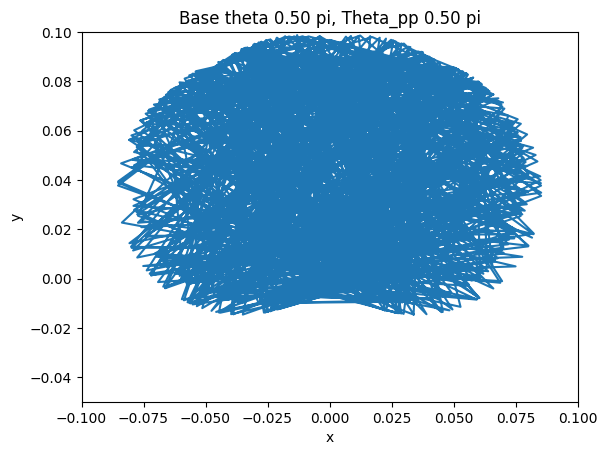
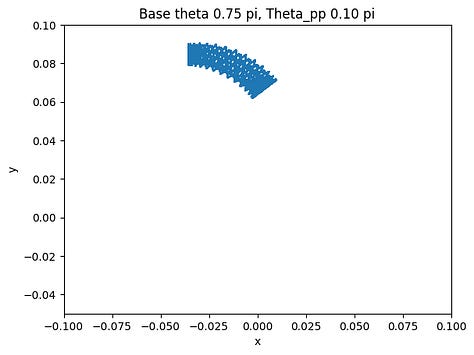
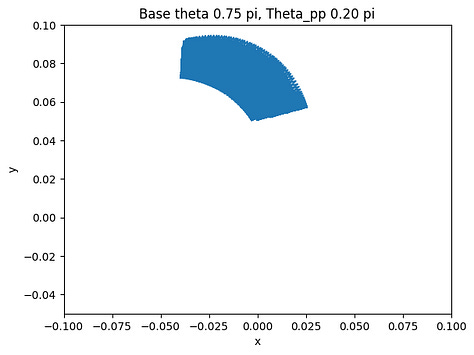
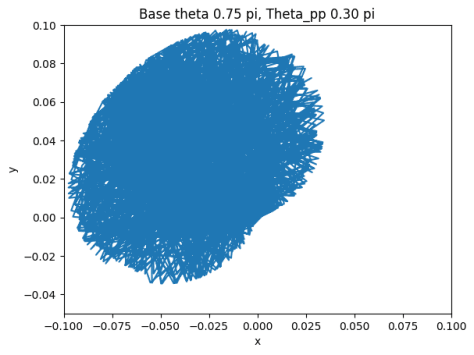
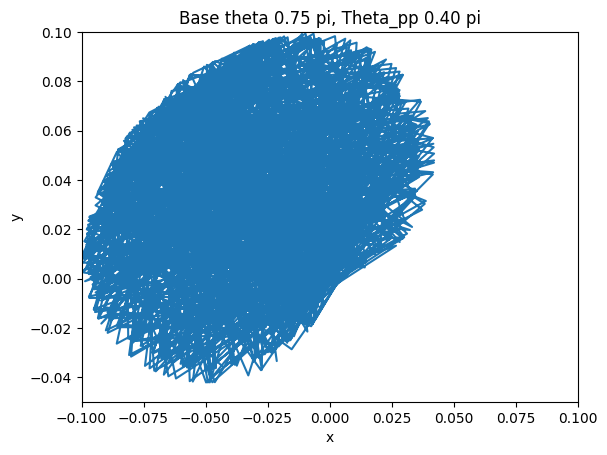
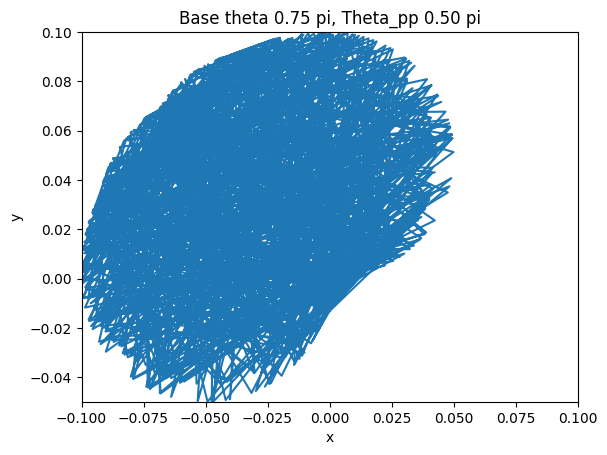
The figures show the range of motion of the mass at the end of the pendulum. As shown above, the smaller the peak-to-peak angle is, the more concrete the motion will be by having a smaller area of the range of motion. On the other hand, if the angle is large, the motion of the mass will be a big cluster of possibilities, which is what we want to avoid if we want the pendulum to have a predictable motion to utilize.